Potenciální a aktuální nekonečno (komentář k teorii množin), část II

Velkolepý matematický chrám, jenž byl zbudován na základech Cantorovy teorie množin, tu neochvějně stojí již 141 let. My se jej dnes - a jsme si plně vědomi míry kacířství, do kterého se pouštíme - pokusíme srovnat se zemí.

                V minulém díle jsme stručně shrnuli problematiku různě velkých nekonečen. Kdo si svým vhledem do uvedené problematiky není jist, tomu nejprve doporučíme náš předchozí text, v němž stručnou a přehlednou formou shrnujeme to nejpodstatnější z teorie množin:

Devadesát let nekonečného ráje (komentář k teorii množin), část I

Potenciální nekonečno a aktuální nekonečno

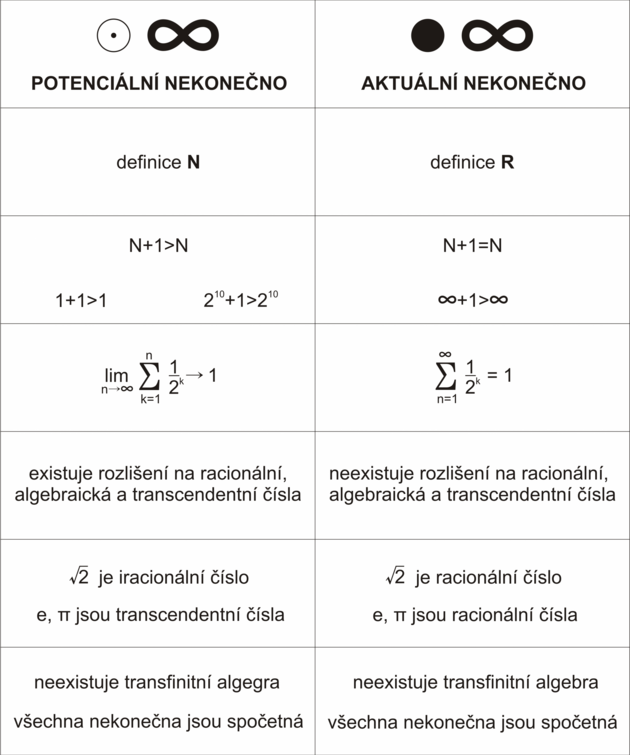
                Pro naši věc je naprosto stěžejní postihnout rozdíl mezi potenciálním a aktuálním nekonečnem. Pro přehlednost zavádíme i vlastní značení. Potenciální nekonečno budeme označovat symbolem 0?, aktuální nekonečno pak symbolem ??. Mělo by se to dobře pamatovat, neboť potenciální nekonečno je kdesi v nedostižné dálce (tečka uprostřed kruhu symbolizuje nedosažitelnost, úběžník), aktuální nekonečno je možno uchopit jako celek (proto plný kruh). Vzhledem k technickým problémům se zobrazováním některých znaků jsme v textu použili prázdný kruh, ale aby bylo zřejmé, jaké označení pro potenciální a aktuální nekonečno zavádíme, přikládáme obrázek:

                Předně: 0? je nedosažitelné, ?? dosažitelné je. Ačkoliv to může vypadat pouze jako zbytečný formalismus, zásadní rozdíl bude ihned zřejmý, ukážeme-li si rozdíl na příkladech.

                Tak třeba řada přirozených čísel není shora nikterak omezena, ovšem v principu neexistuje žádné největší přirozené číslo, neboť existuje snadný způsob, jak najít číslo větší. K libovolně velkému konečnému N lze přičíst 1, čímž získáme číslo N+1>N. Nekonečno je tedy přístupno pouze potenciálně (0).

                S aktuálním nekonečnem (??) je to poněkud složitější, ale ani zde nás nečekají zásadní obtíže. Představme si součet nekonečné řady 1/2 + 1/4 + 1/8 + ... + 1/2N, kde limita N›?. Kdybychom se na problém dívali optikou 0?, museli bychom konstatovat, že součet této řady se s libovolnou přesností blíží 1, ale tohoto součtu nikdy nedosáhne. Podívejme se ale na problém opačně: představme si úsečku délky 1, kterou máme rozpůlit. Operace půlení úsečky je snadná jak matematicky tak geometricky, a v principu je tedy snadno a bezproblémově dosažitelná. I polovina úsečky o délce 1 je však úsečkou a i tu je možno rozpůlit. Vzniknou tak dvě úsečky o délce 1/4, z nichž jednu opět rozpůlíme na 1/8 a 1/8, 1/8 znovu rozpůlíme na 2 úsečky o délkách 1/16 a 1/16, a tak dále můžeme pokračovat až do nekonečna. Vidíme, že půlením půlek úsečky generujeme řadu 1/2 + 1/4 + 1/8 + ... + 1/2N, a jelikož víme, že délka úsečky, kterou jsme začali půlit, je rovna přesně 1, pak také víme, že součet uvedené nekonečné řady je přesně 1. Ano, optika ?? nám umožňuje říct, že součet uvedené řady je přesně roven 1, zatímco optika 0? nám v nejlepším případě umožní tvrdit, že součet této řady se libovolně může přiblížit 1, ale této hodnoty nikdy nedosáhne. Z uvedeného je zřejmé, že rozdíl mezi 0? a ?? je třeba brát vážně.

Jak a kde se objevilo aktuální nekonečno?

                Staří Řekové nejprve znali nekonečno pouze potenciálně (0), ať už se jednalo o tvrzení o rovnoběžkách (dvě rovnoběžné úsečky je možno libovolně dlouho prodlužovat, a přesto se neprotnou; srovnej výklad o rovnoběžkách optikou ??: rovnoběžky se protnou v ?!), o množinu přirozených čísel (N+1>N), či o Erathostenovo síto (neexistuje žádné největší prvočíslo). Zénónův paradox o tom že Achilles nedohoní želvu, však do řecké představy bezmezna (což je možná lepší označení než potenciální nekonečno, už s přihlédnutím k významu tradičního výrazu apeiron) vnáší představu ??, což ve své době pochopitelně nebylo rozpoznáno, a proto byla Zénónem popsaná situace označena slovem paradox a dobrých sto let paradoxem zůstala.

                Případ s aktualizací potenciálního nekonečna lze vystopovat i v Číně; přes pochopitelná kulturně-historická specifika, která nutně vedla k odlišnému formulačnímu pojetí, však paralela s Řeckem vystupuje naprosto zřejmě a evidentně.

                Co se potenciálního nekonečna (či snad, jak jsme již podotkli - bezmezna) týče, používala Říše středu pro nepředstavitelně velká čísla číslovku 10.000. Ta v obecném konsensu nepředstavovala konkrétní číslo, ale číslo libovolně velké, ovšem nepředstavitelně nezměrné. Ve třetím století před naším letopočtem se ve filosofické knize Han Feizi objevuje paralela s tím, co svými provokacemi vykonal Zénón pro ujasnění rozdílu mezi aktuálním a potenciálním nekonečnem.

                Příběh je následující: jakýsi muž se snažil prodat kopí a štít. Když se ho zeptali, jak dobré je to kopí, odpověděl, že prorazí každý štít. Když se jej ptali, jak dobrý je jeho štít, odpověděl, že odolá každému kopí. Když se jej kdosi zeptal, co se stane, když hodí své kopí proti svému štítu, nedokázal odpovědět. Ve zobecněné formě pak tento problém vstoupil do historie formou slavné otázky: Co se stane, když se nezměrná síla střetně s neústupným tělesem? Pokus o porovnání nekonečen, jemuž nutně musí aktualizace nekonečna předcházet, je tu zřejmý. Tímto způsobem tedy bylo ?? představeno v čínské filosoficko-logické tradici.

                My už jsme však dnes o rozdílu mezi  0? a ?? dostatečně poučeni, takže dokážeme bez problémů přijmout, že součet nekonečné řady může být konečný (Zénónův paradox), stejně jako to, že můžeme porovnávat mohutnost dvou nekonečen, jak nás poučil Cantor (kopí a štít).

                Nyní se však už konečně pojďme věnovat slibované herezi.

?2 jako racionální číslo

                Georg Cantor ukázal, že množina všech podmnožin spočetně nekonečné množiny (tedy včetně nekonečných podmnožin) je větší (má větší mohutnost), než původní nekonečno, tedy že má více prvků. Jak vypadá taková nekonečná podmnožina? Je to například množina všech přirozených čísel bez čísla 3.852, množina všech prvočísel, množina všech lichých čísel plus čísla 2 a 3.888.526.828, atd. Z uvedeného jednoznačně vyplývá, že Cantor používá nekonečně velké množiny jako prvky. Existence nekonečně velkých množin je však, jak jsme si řekli, doménou ??, gramatice 0? žádný prostor pro reálnou existenci nekonečných množin neexistuje.

                A nyní k našemu problému: ?2 je tradičně chápána jako číslo iracionální, neboť neexistují dvě libovolně velká, ale konečná čísla (tedy optika 0?), jejichž podílem by právě ?2 byla. Nicméně - a navazujeme na předchozí tvrzení - není důvod, aby neexistovala dvě nekonečná čísla , jejichž podílem je právě ?2.

                Závěr je zřejmý: díváme-li se na problém (i)racionality čísla ?2 optikou 0?, jedná se o číslo iracionální, díváme-li se na totéž číslo optikou ??, pak se zcela přirozeně jedná o číslo racionální.

? jako algebraické číslo

                Existuje řada druhů čísel. Základem budiž přirozená čísla a nula, ať se nezdržujeme (-8527, -3, 0, 1, 2, 3, 56 ... atd. tedy všechna čísla, která lze přičítáním či odečítáním čísla 1 odvodit z čísla 1). Pak tu jsou racionální čísla (sem spadají jednak všechna přirozená čísla, ale dále se tu vyskytují čísla jako 1/2, 13/7, 1.000.006/8.341, atd., ale i čísla 0/1, 1/1, -3/1, atd.).

                 Je tedy zřejmé, že množina přirozených čísel je podmnožinou množiny racionálních čísel. Dle tradičního výkladu, který jsme právě zpochybnili, je ?2 iracionální číslo, neboť evidentně se o číslo jedná, ale nelze jej vyjádřit formou zlomku. Z tohoto pohledu je tedy množina racionálních čísel podmnožinou takové množiny, v níž vystupují vedle zlomků i čísla jako ?2, ?3, ?, atd. Za algebraická čísla se označují taková čísla, která jsou kořenem diofantské rovnice, tedy rovnice, v níž vystupují celočíselné koeficienty. Dle tradičního výkladu je ?2 algebraickým číslem, neboť je kořenem rovnice X2=2. Číslo ? však algebraickým číslem není, neboť neexistuje taková rovnice s celočíselnými koeficienty, jejímž kořenem by bylo právě číslo ?. Čísla, která nejsou algebraická, se označují jako transcendentní.

                Analogickou argumentací jako výše (v případě důkazu, že ?2 je optikou ?? racionální číslo)   lze snadno ukázat, že i ? je číslo racionální.

                Pokud se na ? díváme optikou 0?, pak se skutečně jedná o číslo iracionální, nealgebraické, přesto však je to reálné číslo (transcendentní číslo). Pokud však zvolíme optiku ?? (a znovu opakujeme, že tato optika je právoplatná, neboť bez ní by Cantor nemohl sestrojit množinu všech podmnožin dané množiny), pak musíme dojít k tomu, že existují dvě nekonečná čísla, jejichž poměrem je přesně ?. Evidentně jsou to čísla 3141592›... a 1000000›... V optice aktuálního nekonečna je tak ? zcela přirozeně číslem jak algebraickým, tak racionálním.

                Ve výše uvedeném není žádný rozpor, neboť v optice ?? rozdíly mezi racionálními, algebraickými a transcendentními čísly mizí. Tyto rozdíly jsou vlastní pouze optice 0?. To je naprosto radikální tvrzení, které staví na hlavu posledních 141 let teorie množin!

Právoplatnost optiky ??

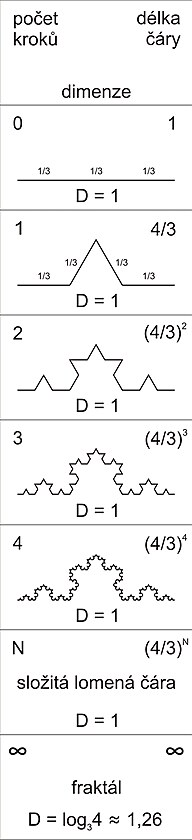
                Pokud by snad někdo stále váhal, zda můžeme na čísla jako ?2 nebo ? svévolně uplatňovat optiku ??, zopakujeme, že tato optika je pro řadu oblastí matematiky naprosto nepostradatelná. Uvedli jsme příklad s půlením úsečky, ten však nemusí být dostatečně názorný, proto se na chvíli pozastavíme u fraktálů. To jsou geometrické útvary, které vzniknou teprve v okamžiku, když aktuálně provedeme ? iterací. Do té doby (tedy pokud je iterací pouze 0?, tedy libovolně mnoho, ale konečně), se nejedná o fraktál, ale pouze komplikovanou euklidovskou geometrii, v jejímž rámci mají linie dimenzi 1, plochy dimenzi 2 a prostor dimenzi 3. Teprve aktuální aplikací nekonečného množství kroků vzniká fraktál (který své jméno získal právě proto, že dimenze takového objektu není celočíselná, ale jiná).

                Obdobně se bez gramatiky  ?? neobejdou součty nekonečných konvergentních řad, limity, infinitezimální počet, na němž stojí například odvození vzorců pro obvod elipsy nebo objem koule, atd.

Cantorův diagonální důkaz optikou  0? a ??

                Takto vyzbrojeni se konečně můžeme důstojně utkat se slavným Cantorovým diagonálním důkazem, s nímž stojí a padá celá mohutná stavba různě velkých nekonečen.

                Z předchozího výkladu (I.díl textu) je zřejmé, že Cantorův diagonální důkaz se opírá o výklad skrze 0?, neboť k libovolně dlouhému seznamu čísel můžeme neomezeně přidávat čísla další a další. To samo o sobě problém není, Cantor si prostě zvolil jeden ze dvou přípustných nástrojů (připomínáme pouze, že každý z nich má svou gramatiku, a tyto gramatiky nejsou beze zbytku kompatibilní, takže není záhodno je svévolně zaměňovat). Problém, a to přímo kardinální, nastává v okamžiku, kdy se zamyslíme, zda i množina všech (tedy i nekonečných) podmnožin množiny přirozených čísel je konstruována v prostředí 0?. Odpověď musí být záporná, neboť v tomto důkazu - a to zcela evidentně - pracujeme s gramatikou ??. Nepoužíváme totiž pouze libovolně velká (ale konečná!) čísla, ale při konstrukci množiny všech (tedy i nekonečných!) podmnožin množiny přirozených čísel manipulujeme s čísly aktuálně nekonečnými! V tom je ihned zřejmý metodologický rozpor! Zkusme se tedy důsledně držet nejprve jedné, a potom druhé metody.

                Cantor optikou 0?: Potenciální nekonečno z principu zabraňuje používat aktuálně nekonečné množiny, takže nám tedy ani nedovoluje vytvořit množinu všech (tedy včetně aktuálně nekonečných) podmnožin dané množiny. Skrze 0? tedy cesta k různě velkým ? nevede (mimo jiné i proto, že množina všech pouze konečných podmnožin množiny přirozených čísel má stejnou mohutnost jako množina přirozených čísel, což je metodologicky opodstatněné tvrzení, neboť jak množinu přirozených čísel, tak každou konečnou podmnožinu jsme schopni zkonstruovat pouze s použitím gramatiky 0?).

                Cantor optikou ??: Ukázali jsme, že Cantorův diagonální důkaz je prováděn skrze gramatiku 0?. Zkusme jej modifikovat tak, abychom jej mohli provést s použitím gramatiky ?? (Cantorův důkaz jsme podrobně rozebrali v minulém díle a použili jsme takovou jeho modifikaci, která se vztahuje na interval [0,1]; přiložené obrázky podporují názornost). Pouze takto provedený diagonální důkaz totiž můžeme použít metodologicky správně, totiž v kombinaci s tvrzením o množině všech podmnožin dané množiny, které se odehrává v prostoru ??.

                Pojďme tedy sestrojit aktuálně nekonečný seznam všech čísel v intervalu [0,1]: V takovém seznamu nutně musí existovat čísla, která mají pouze jedno desetinné místo. Jsou to čísla 0,0 - 0,1 - 0,2 - 0,3 - ... 0,9. Tím jsme vyčerpali všechna čísla která mají pouze 1 desetinné číslo. Ve druhém kroku vypíšeme všechna čísla, jejichž desetinný rozvoj zabírá 2 desetinná místa, a která jsme dosud neuvedli v našem výčtu. Jsou to čísla 0,00 - 0,99, ovšem právě bez čísel 0,00 - 0,10 - 0,20 - ... - 0,90. Poté můžeme vypsat všechna čísla, jejichž desetinný rozvoj zabírá právě 3 desetinná místa, ovšem bez čísel, která jsme již v seznamu uvedli v předchozích dvou krocích. Je evidentní, že takto můžeme pokračovat libovolně dlouho, tedy pro libovolný počet desetinných míst, a to včetně čísel, jejichž desetinný rozvoj je nekonečný (to je nezbytné, chceme-li důkaz provést v prostředí  ??).

                Takový seznam obsahuje všechna čísla, tedy nejen čísla racionální, ale i čísla algebraická a transcendentní (tedy včetně ?2 a ?!). Jelikož náš seznam aktuálně(!) obsahuje všechna(!) čísla, pak je nutným důsledkem fakt, že nepřipouští konstrukci takového čísla, které by v uvedeném seznamu nebylo. Tím jsme prokázali, že důsledné dodržování gramatiky ?? v celém Cantorově důkazu opět nevede ke vzniku čísla, které by nebylo obsaženo v našem seznamu všech čísel (včetně čísel, jejichž desetinný rozvoj je aktuálně nekonečný).

                Pro stručný přehled právě řečeného jsme připravili přehlednou tabulku (rozdíl v definici přirozených čísel N a reálných čísel R bude přiblížen níže):

Shrnutí

                Z výše uvedeného se zdá vyplývat, že jakákoliv nekonečná množina je spočetná. To znamená, že jakoukoliv množinu čísel (včetně množiny všech reálných čísel) lze vzájemně jednoznačně zobrazit na množinu přirozených čísel. Jsou-li naše úvahy správné, pak je třeba uzavřít následovně:

                Cantor udělal stejnou chybu jako Zénón, když nebyl schopen od sebe důsledně odlišit 0? a ??. Zénónova neschopnost odlišit 0? a ?? je omluvitelná, neboť Zénón ?? svými úvahami představil světu matematiky, respektive minimálně vykročil na cestu, která k uvědomění si rozdílu mezi 0? a ?? vede. S odstupem staletí nám Zénónův paradox přestal připadat jako singularita, v níž kolabuje logika, jako paradox, neboť jsme z odstupu a z nadhledu nakonec pochopili, kde Zénón ve svých úvahách udělal pochopitelnou a omluvitelnou chybu. Jeho logická hříčka ve finále vedla ke vzniku infinitezimálního počtu, který právem patří k pokladům světové matematiky, a nikdo dnes nezpochybňuje Zénónův význam pro dějiny matematiky.

                Georg Cantor místo Zénónova paradoxu vytvořil ráj transfinitní algebry. A David Hilbert věřil, že nikdo už nikdy matematiky z tohoto cantorovského ráje nevyžene. Podmínky, za nichž vznikl Cantorův ráj transfinitní algebry, vychází ze stejného problému, jako Zénónův paradox - z neschopnosti dostatečně důsledně od sebe odlišit 0? a ?? - a analogicky i tento ráj musí skončit.

                Teď, když je jádro problematičnosti Cantorovy úvahy odhaleno, je možno se zpětně pousmát nad jeho naivitou, obdobně jako se dnes s přirozenou samozřejmostí pousmíváme nad tím, že Achilles, nejrychlejší běžec starověku, není schopen dohonit želvu, která rychlostí pohybu rozhodně nevyniká.

Obhajoba Cantora místo závěru

                Domníváme se, že výše řečené může znít vůči Georgu Cantorovi, k němuž navzdory naší polemice s jeho vývody chováme bezmezný obdiv, neuctivě. Považujeme za vhodné se zamyslet nad tím, kde nedopatření, které Cantorovi vyčítáme, mohlo vzniknout. A znovu si na pomoc vezmeme 0? a ??.

                Množina přirozených čísel byla vždy tradičně chápána jako množina potenciálně libovolně velká, bez horního omezení, tedy optikou 0?. Naproti tomu je zřejmé, že vezmeme-li si nějakou konečnou úsečku IABI, tak tato úsečka má nekonečné množství bodů aktuálně, neboť je vidíme všechny najednou, a kterýkoliv z nich je aktuálně dostupný, dokonce i ten ze všech nejposlednější bod B. Dále: Již od dob Euklida je přímka chápána jako neomezené protažení úsečky. A zde se dostáváme k jádru problému: Úsečku sice protahujeme neomezeně, aniž bychom však byli schopni dobrat se jejího konce (0?), zatímco úsečka samotná již má formu ??. Pokud tedy gramatiku 0? aplikujeme na ??, nemůžeme získat objekt, který by byl 0?, ale pouze objekt, který je ??.

                Cantorův důkaz existence různě velkých nekonečen tedy od začátku spočíval na přehlédnutí skutečnosti, že množina přirozených čísel má od začátku formu 0? a množina reálných čísel - jak jsme právě ukázali - formu ??. Cantor tedy neporovnával různě velká nekonečna (což se zdálo být záměrem i důsledkem jeho diagonálního důkazu), ale dva různé přístupy k nekonečnu, porovnával potenciálně chápané nekonečno přirozených čísel s aktuálně chápaným nekonečnem reálných čísel. Z tohoto pohledu je tedy pochopitelné, proč mu vyšlo, že existují různě velká nekonečna. Kdyby totiž vzal přirozená čísla aktuálně, musel dojít k závěru, že aktuálně nekonečná množina přirozených čísel je stejně velká jako aktuálně velká množina reálných čísel.

                V našem textu jsme ukázali, že důsledným dodržování jedné ani důsledným dodržováním druhé gramatiky nemůžeme vytvořit žádné "větší" nekonečno. Závěr je tedy nasnadě: matematika byla vyhnána z iluzivního ráje transfinitní matematiky, a byla navrácena do ráje bezmezného, tedy jediného nekonečna.   

Dominik Herezán